我们先上点干货吧。啊哈啊哈哈~
我们先来看看百度百科对它的定义:
核函数指所谓的径向基函数,就是某种沿径向对称的标量函数(其实具指的是高斯核)。
通常定义为空间中任一点x到某一中心xc之间的欧式距离的单调函数,可记作k(||x-xc||),其作用往往是局部的,即当x
远离xc时函数的取值很小。
然后官方定义:
设X为输入空间(欧氏空间或离散集合),H为特征集合(希尔伯特空间),如果存在一个从X到H的映射,φ(x):X→H,使得所有的
x,y∈X,函数K(x,y)=φ(x)▪φ(y)。则称K为核函数,φ(x)为映射函数,φ(x)φ(y)为x,y映射到特征空间上的内积。
正文开始之前,我们还得说明白一些专业术语,免得显得那么晦涩。
欧氏空间:
定义:
设V是实数域R上的线性空间(或者称为向量空间),若V上定义着正定对称双线性g(g称为内积),则V称为内积空间或者
欧几里得空间,具体的说,g是V上的一个二元实值函数,满足下述关系:
(1)g(x,y)=g(y,x);(对称性)
(2)g(x+y,z)=g(x,z)+g(y,z);(第一变元线性性)
(3)g(kx,y)=kg(x,y);(第一变元线性性)
(4)g(x,x)>=0,而且g(x,x)=0当且仅当x=0时成立。(正定性)
这里x,y,z是V中任意向量,k是任意实数。
希尔伯特空间:n维欧几里得空间的推广,可以看作是无限维的欧几里得空间,且具有完备性(直白点说,完备性就是指
在空间的极限运算中,我们的极限不会取出去)。
便于理解一些经常出现的词汇,奉上一个上海交大公开课的一个讲解的图片:
············································手动分割··················································
上面就是一些晦涩的数学概念,看起来很恐怖,那就来通俗理解一下好了。
ps:纯属个人理解,可能不够专业吧。
我们所学的大部分数学课程都是以集合开始的,其实这就是近代直到现代我们研究数学的基础,学习数学,研究数学,就相当于
把我们现实世界存在的,看似不存在(无法感知)的东西抽象成集合,然后从不同的角度,不同的路径出发,进行研究。
空间,就是拥有结构的和规则的集合。
我们从初中开始接触坐标系,其实就已经潜移默化的接受空间的概念了,直角坐标系中有x轴,y轴,我们可以坐标化平面上
任意一点的位置,一个平面可以看作是由无数个点组成,而任意一个点都在我们的坐标系的”大网”之中。
现实世界是一个三维空间,如果我们规定一个远点,并且规定三个方向,分别取名x,y,z,然后规定它们相互垂直,那么我们每个人,
的位置就可以唯一确定了。这三个方向,就是我们所谓的基的概念(之前在线性代数里很多见,其实矩阵就是一种描述工具)。
有了对位置的描述,但是我们的元素并没有所谓的长度,于是乎,又在上面的空间当中引入特殊的长度,名为范数。
在此至上,又继续引入了角度的概念,于是又有了内积的概念。
继续的继续,引入极限的概念,但是我们所计算的极限可能跑出我们的给定的空间,所谓引入完备性,就有了我们上面所说的
希尔伯特空间。具体所需,据其所提。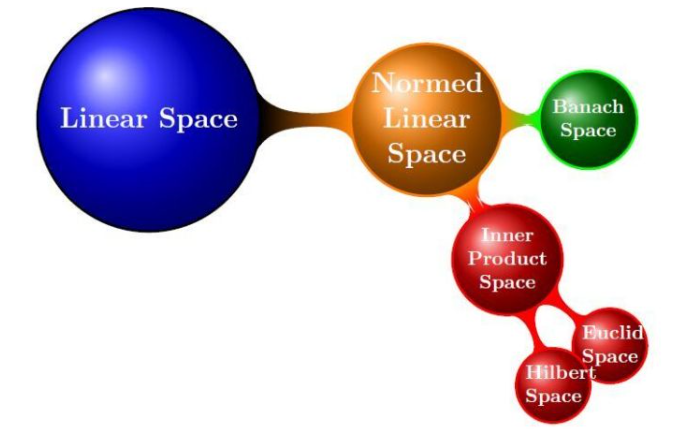
············································手动分割··················································
进入正题了,那么我们的核函数到底是干什么的呢。
看上面,就是想从欧氏空间映射到希尔伯特空间,也就是从低维空间映射到高维空间。
便于理解,我在网上找了一个例子,原文参照:
https://www.cnblogs.com/hezhiyao/p/7238500.html
我们看下面这幅图:
这幅图位于第一,第二象限内,讲红色门上的点看作“+”数据,紫色的字上的点看作“-”数据,它们的横纵坐标就是两个特征,
很明显,我们并找不到一条直线来将+-两中数据分开,也就是在这个二维空间当中,+-数据线性不可分。
那么我们现在考虑核函数:
这里面v1=(x1,y1),v2=(x2,v2),是二维空间中的两点,这个核函数对应着一个二维空间到三维空间的一个映射,
表达式为: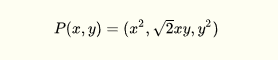
在P这个映射下,原来的二维空间中的图就会变成下面这个样子: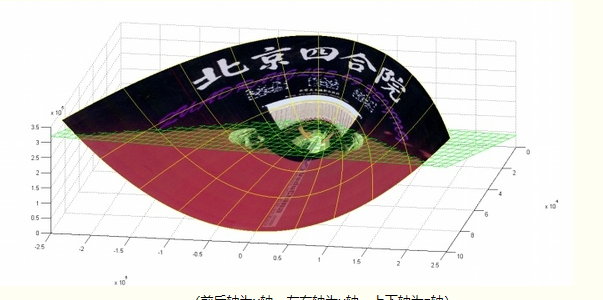
图中绿色的平面就可以完美的将红色和紫色的数据分割开来,两类数据在三维空间中就线性可分了。
对应到我们的平面空间当中,这个平面的其实是一条双曲线,并不是线性的。
这个例子中,我们将二维空间映射到三维空间中,这是我们通过感官可以直接感受出来的,其实在我们的事实中,
它们的映射并不一定可以显式的表现出来,我们映射到的空间的维数可能高得多,甚至是无穷维的。
在我们进行使用的时候,选择核函数是很重要的一步,要根据实际而定。
接下来,如果我对核函数的选择又更近一步的认识,会分享在这里的。
