<学习笔记> 线性回归

2018-04-19

之前我们构造了各类分类器，目的是分类，目标变量是标称型数据，从这一篇开始，开始
对连续型数据进行预测，那么我们通过什么方法进行呢，那就是回归。
我们利用回归寻找两种或两种以上变量间的相互依赖关系。
回归在化学分析，遗传学等我们常见的学科当中有着非常广泛的应用。
这篇文章主要对线性回归进行学习总结。

一.利用线性回归找到最佳拟合直线
回归的目标是预测数值型的目标值。
最直接的方式是通过输入写出一个目标的表达式：

y=ax+b;

这就是所谓的回归方程，其中的a,b可以被称作回归系数。
我们求得回归系数的过程就是回归。
一旦我们知道了a,b两个值的大小，如果给定输入x，那么结果y就很容易得到了。
那么怎样从一大堆的数据中求出回归方程呢，假设输入矩阵放入矩阵x中，而回归系数存放在向量
w中，那么对于给定的数据X1，预测结果将会通过

1	Y1=(X1^T)*w

给出，现在的问题是，我们给出的是一系列的x和y，要得到的是w，一个常用的方法是得到误差最小的
w。这里的误差是指预测y和实际y之间的差距，直接使用该误差的简单累计会使得结果相互抵消，所以
我们将其平方化处理，采用平方误差。
那么平方误差即可写作：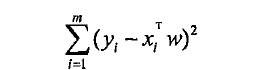

如果是用矩阵表示的话，那么可以写作：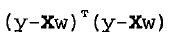

都w求导，得到X^T(Y-Xw),令其等于0，接触w如下：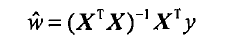

w头上有个小标记，代表这是当前可以估计出的w的最优解。从现有数据估计出的w可能与真实的w
值有一定的差异，这个解只是代表一种当前的最优估计，因此要加以区分。
还要注意上面的计算涉及到矩阵求逆，那么这个方程只有在逆矩阵存在的条件下才适用，
所以我们编写代码的时候要进行判断。
下面是用python实现的标准回归函数以及数据读取函数：

from numpy import *
def loadDataSet(filename):
    numfeat=len(open(filename)
                .readline().split('\t'))-1
    dataMat=[]
    labelMat=[]
    fr=open(filename)
    for line in fr.readlines():
        lineArr=[]
        curLine=line.strip().split('\t')
        for i in range(numfeat):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(curLine[-1])
    return dataMat,labelMat
def standRegres(xArr,yArr):
    xMat=mat(xArr)
    yMat=mat(yArr).T
    xTx=xMat.T*xMat
    if linalg.det(xTx)==0.0:
        print("this matrix is singular,cannot do inverse")
        return
    ws=xTx.I*(xMat.T*yMat)
    return ws

上面的数据载入不用过多介绍，第二个函数只用几行代码就实现了我们上面要求的结果，
先将数据向量矩阵化，然后计算平方，通过调用linalg模块求行列式，如果行列式为0，
那么矩阵不可逆，反之，计算结果。
几乎任意的数据点都可以用上述的方法建立模型，但是如何评价我们模型的好坏呢。
对于下面两个图，我们在这两个数据集上分别做线性回归，将得到完全一样的拟合直线。
显然两个数据是不一样的，那么模型分别在二者的效果比较起来如何。
有一种方法就是比较预测值和真实值之间的匹配程度，计算两个序列的相关系数。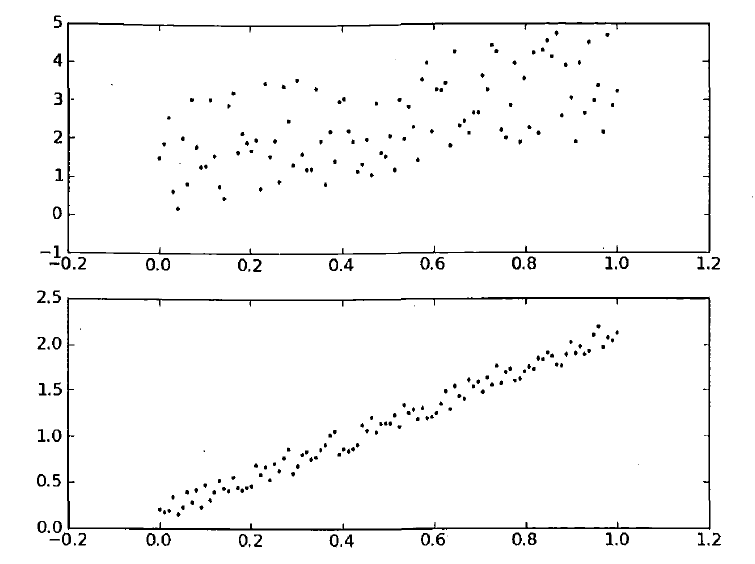

上面的两个图具有相同回归系数(0,2.0)，但是上图的相关系数是0.58，
下图的相关系数达到了0.99。
numpy库中提供了计算相关系数的方法：
通过corrcoef(yEstimate,yActual)来计算预测值和真实值之间的相关性。

上面我们将数据当作直线来建模，寻找了最佳拟合曲线，我们还可以发现数据当中存在的潜在模式。

二.局部加权线性回归
线性回归会遇到的问题是有可能出现欠拟合现象，因为它要求的是具有最小均方误差的无偏估计。
显然，欠拟合会使得我们得不到好的结果。所以我们要想办法引入一些偏差，来降低我们的均方误差。
其中的一种方法就是局部加权线性回归(LWLR)。
在这个算法当中，我们基于预测点附近的的每个点一定的权重，然后在这个子集上，进行普通的回归。
该算法解出的回归系数w的形式如下：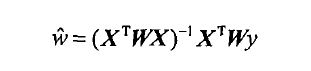

其中w是一个权重，用来给每个数据点赋予一个权重，
LWLR使用类似SVM核的“核”来对附近的点基于更高的权重，核的类型可以自由选择，
高斯核对应的权重如下：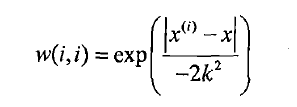

那么很容易看出来，点x与x(i)越近，w(i,i)将会越大。
我们可以通过调节上式中的k值，来决定我们对附近的点给予多大的权重。
下图展示了参数k与权重的关系。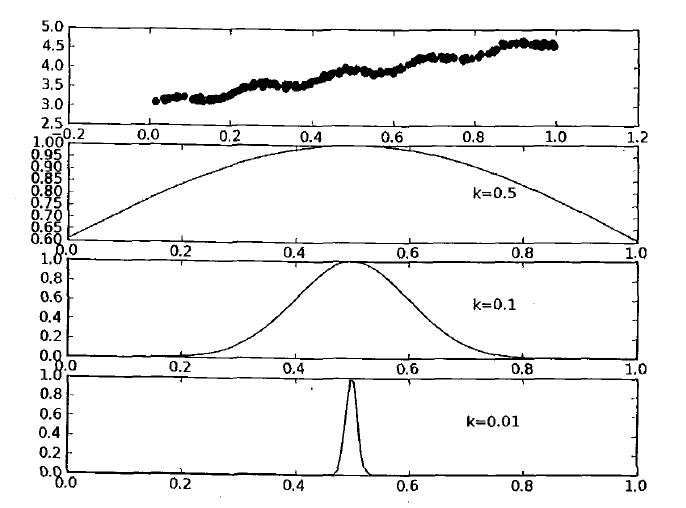

从图中可以观察得出，当k值越大的时候，越多的数据用于训练回归模型。
下面给出局部加权线性回归函数的代码：

def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat=mat(xArr)
    yMat=mat(yArr).T
    m=shape(xMat)[0]
    weights=mat(eye((m)))
    #创建对角权重矩阵，随着样本点与待估测的点的距离的递增，权重将指数级递减。
    for j in range(m):
        diffMat=testPoint-xMat[j,:]
        weights[j,j]=exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx=xMat.T*(weights*xMat)
    if linalg.det(xTx)==0.0:
        print("cannot inverse")
        return
    ws=xTx.I*(xMat.T*(weights*yMat))
    return testPoint*ws
def lwlrTest(testArr,xArr,yArr,k=1.0):
    m=shape(testArr)[0]
    yHat=zeros(m)
    for i in range(m):
        yHat[i]=lwlr(testArr[i],xArr,yArr,k)
    return yHat

得到的拟合直线如下图：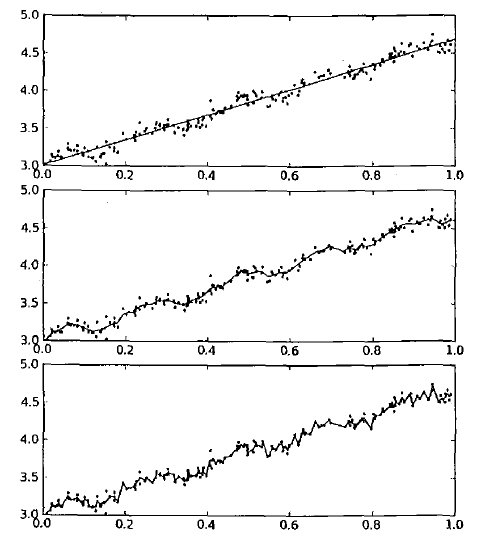

第一幅图取k=1.0,所有数据等权重，最佳拟合直线与标准回归一致。
第二幅图取k=0.01，抓住了数据的潜在模式，得到了很好的结果。
第三幅图取k=0.003,纳入了很多的噪声点，拟合的直线与数据点过于靠近了，
这就是个过拟合的例子。而第一幅图是一个欠拟合的例子。
所有我们在选择k的时候，并不是越大或者越小越好，而是要通过对比不同的模型，来综合
考虑我们选取的参数值，找到最佳模型。

三.缩减系数来理解数据
有时候我们会遇到数据特征比样本点还多的情况，如果使用之前的方法来进行计算，会出错，
特征比样本点还多，说明输入数据的矩阵不是满秩矩阵，非满秩矩阵求逆会出现很多问题。
为了解决这个问题，引入了“岭回归”，这是其中一种缩减方法，
除此之外，还有lasso法，这种方法效果最好但是最复杂。
最后还有一种“前向逐步回归”,既能得到满意的效果，也容易实现。

1.岭回归
岭回归就是在矩阵X.TX加上一个λE使得矩阵非奇异。当X非满秩，或者是矩阵的列与列之间的
相关性太高的话，也就是X.TX接近奇异的时候，计算(X.T*X)的逆的时候误差会很大。
在这种情况下，回归系数的计算公式为: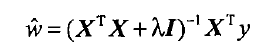

岭回归最初用来处理特征数多于样本数的情况(直观上就是矩阵不满秩)，现在也用于在估计
中加入偏差，来得到更好的估计，通过引入λ来限制所有w的和，通过引入该惩罚项，
减少不重要的参数，这个技术就是缩减。

训练方法类似，通过预测误差最小化得到λ：
得到数据集，一部分测试，剩余的用来训练参数w。
训练后用用测试集预测回归性能。
通过选取不同的λ重复上述过程，最终选取使得误差最小的值。
代码实现:

def ridgeRegres(xMat,yMat,lam=0.2):
    xTx=xMat.T*xMat
    denom=xTx+eye(shape(xMat)[1])*lam
    if linalg.det(denom)==0.0:
        print("this matrix is singular,cannot do inverse")
        return
    ws=denom.I*(xMat.T*yMat)
    return ws
def redgeTest(xArr,yArr):
    xMat=mat(xArr)
    yMat=mat(yArr).T
    yMean=mean(yMat,0)
    yMat=yMat-yMean
    xMeans=mean(xMat,0)
    xVar=var(xMat,0)
    xMat=(xMat-xMeans)/xVar
    #标准化,减均值，初方差；
    numTestPts=30
    三十个不同lambda值进行测试；
    wMat=zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        ws=ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat

2.前向逐步回归
属于一种贪心算法，因为每一步都尽可能的减小误差。
一开始，所有的权重都设置为1，然后每一步所做的决策是对某个权重增加或减少一个很小的值。
代码实现:

1
2
3

def rssError(yArr,yHatArr):
    return ((yArr-yHatArr)**2).sum()
#预测误差大小；

def regularize(xMat):
    xVar=var(xMat,0)
    xMeans=mean(xMat,0)
    xMat=(xMat-xMeans)/xVar
    return xMat
#标准化；

def stageWise(xArr,yArr,eps=0.01,numIt=100):#迭代步长，迭代次数；
    xMat=mat(xArr)
    yMat=mat(yArr).T
    yMean=mean(yMat,0)
    yMat=yMat-yMean
    xMat=regularize(xMat)
    m,n=shape(xMat)
    returnMat=zeros((numIt,n))
    ws=zeros((n,1))
    wsTest=ws.copy()
    wxMax=ws.copy()
    for i in range(numIt):
        print(ws.T)
        lowestError=inf
        for j in range(n):
            for sign in [-1,1]:
                wsTest=ws.copy()
                wsTest[j]+=eps*sign
                yTest=xMat*wsTest
                rssE=rssError(yMat.A,yTest.A)
                if rssE<lowestError:
                    lowestError=rssE
                    wsMax=wsTest
        ws=wsMax.copy()
        returnMat[i,:]=ws.T
    return returnMat

当我们应用缩减方法时，模型也就增加了偏差，与此同时减少了模型的方差。
在这之后，我们就要权衡偏差与方差，是我们的模型得到更进一步的优化。