<学习笔记> AdaBoost元算法

元算法就是对其他算法进行组合的一种方式。
bagging方法：自举汇聚法，从原始数据中选择s次之后得到s个新数据的技术。新数据集和原数据集的
大小相等。每个新数据集中的数据都是通过在原数据集随机选择来进行替换得到的。
boosting方法：类似bagging，boosting不同分类器权重不同，而bagging相同。
adaboosting运行过程：
训练数据中的每个样本，并赋予一个权重，这些权重构成了向量D。一开始，这些权重都初始化为相等的值。
首先在训练中训练出一个弱分类器并计算该分类器的错误率，然后再同一个数据集上再次训练弱分类器。
在分类器的第二次训练当中，将会调整每个样本的权重，第一次分对的样本的权重降低，分错的权重升高。
为了从所有的弱分类器中获得最终的分类结果，adaboosting为每个分类器都分配了一个权重alpha，
这些alpha值是基于每个弱分类器的错误率进行计算的。
错误率e就是分类错样本数目的和总样本数目的比值。
alpha的计算公式：

1
α=1/2ln(1/e-1)

adaboosting算法的流程可以用下面的图表示：

计算出alpha值之后，就要对我们的向量D进行更新，D的计算方式如下：

计算出D之后，算法开始下一轮迭代，就这样不断重复训练调整权重，边界就是训练错误率为0或者
弱分类器的个数达到指定的值为止。

基于单层决策树构建弱分类器
之前已经接触过了决策树，那么单层决策树就是仅基于单个特征，只有一个分叉过程，也叫做决策树桩。

1
2
3
4
5
6
7
8
9
def loadimpdata():
    datamat=matrix([
        [1.,2.1],
        [2.,1.1],
        [1.3,1.],
        [1.,1.],
        [2.,1.]])
    classlabels=[1.0,1.0,-1.0,-1.0,1.0]
    return datamat,classlabels

上面是我们构造的数据集，将datamat中的数对放入我们的坐标轴，如果想要找到一条平行与坐标轴的直线来将所有的
1型和-1型分开，显然不可能。AdaBoost需要将多个单层决策树结合才能对该数据集进行分类。
上面是数据载入的函数，接下来，要构建多个函数lai建立单层决策树。
第一个函数用于测试是否存在某个值小于或者大于我们正在测试的阈值。
第二个函数用来找到错误率最低的单层决策树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
def stumpclassify(datamatrix,dimen,threshval,threshIneq):
    retarray=ones((shape(datamatrix)[0],1))
    if threshIneq =='lt':
        retarray[datamatrix[:,dimen]<=threshval]=-1.0
    else:
        retarray[datamatrix[:,dimen]>threshval]=1.0
    return retarray
def buildstump(dataarr,classlabels,D):
    datamatrix=mat(dataarr)
    labelmat=mat(classlabels).T
    m,n=shape(datamatrix)
    numsteps=10.0
    beststump={}
    bestclassest=mat(zeros(m,1))
    minerr=inf
    for i in range(n):
        rangemin =datamatrix[:,i].min()
        rangemax =datamatrix[:,i].max()
        stepsize=(rangemax-rangemin)/numsteps
        for j in range(-1,int(numsteps)+1):
            for inequal in ['lt','gt']:
                threshval=(rangemin+float(j)*stepsize)
                predictedvals=stumpclassify(datamatrix,i,threshval,inequal)
                errarr=mat(ones(m,1))
                errarr[predictedvals==labelmat]=0
                weightederror=D.T*errarr#计算加权错误率
                if weightederror<minerr:
                    minerr=weightederror
                    bestclassest=predictedvals.copy()
                    beststump['dim']=i
                    beststump['thresh']=threshval
                    beststump['ineq']=inequal
    return beststump,minerr,bestclassest

第一个函数的结构很简单，不做过多解释。
第二个函数最重要的部分就在三层循环的部分，
第一层循环在数据集的所有特征上遍历，通过计算最大值和最小值我们来得知需要多少步长。
第二层循环是在上面选取的值上进行遍历。
可以将阈值设置为整个取值范围之外可以，所以需要额外的步骤。
第三层循环是在大于和小于之间切换不等式。
在最内层循环之中，在数据集以及三个循环变量上面使用第一个函数，基于循环变量，返回分类结果，
接下来构造一个列向量errarr，如果预测值和真实的label值不同，那么填1，然后将错误向量和权重D
相乘，那么就得到了加权错误率，这里就是adaboost和分类器交互的地方，D就是用来评价分类器的。

完整adaboost实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def adaboosttrainDS(dataarr,classlabels,numIt=40):
    weakclassarr=[]
    m=shape(dataarr)[0]
    D=mat(ones((m,1))/m)
    aggclassest=mat(zeros((m,1)))
    for i in range(numIt):
        beststump,error,classest=buildstump(dataarr,classlabels,D)
        print("D:",D.T)
        alpha=float(0.5*log((1.0*error)/max(error,1e-16)))
        beststump['alpha']=alpha
        weakclassarr.append(beststump)
        print("classest:",classest.T)
        expon=multiply(-1*alpha*mat(classlabels).T,classest)
        D=multiply(D,exp(expon))
        D=D/D.sum
        #为进行下一次迭代计算D
        aggclassest+=alpha*classest
        print("aggclassest:",aggclassest)
        aggerrors=multiply(sign(aggclassest)!=mat(classlabels).T,ones((m,1)))#sign()函数：正负分离；
        errorrate=aggerrors.sum()/m
        print("total error:",errorrate,"\n")
        if errorrate==0.0:
            break
    return weakclassarr

上面的函数的参数包括数据集，类别标签以及迭代次数，迭代次数由用户指定。
如果我们在预设的迭代次数未到达之前就达到errorrate为0，那么就直接退出迭代，不需要指定的那么多了。
上面我们融合的是单层决策树，也就是将其作为基分类器。
我们可以通过修改代码将其修改为其他的弱分类器，前面的任何一种都可以。
向量D非常重要，包含了每个数据点的权重，一开始，赋予了每个权重值相同的值，在后续的迭代中，adaboost
会在增加错误分类的数据的权重的时候，降低分类正确的数据的权重。
D是一个概率分布的向量，因此所有的元素之和为1.0。为了满足这个需求，那么一开始就将他切为1/m。
同时，程序还会建立一个列向量aggclassest，来记录每个数据点的类别估计累积值。
adaboost算法的核心在于for循环，该循环运行指定次数或者直到错误率为0退出。
循环中的第一件事是建立单层决策树。随后是计算alpha的值，这个值告诉总分类器这次的单层决策树的
结果的权重，其中的max函数用来避免除零异常。
然后，将这个值加入到beststump字典中，这个字典又加入到列表中。
多个分类器得出结果后，就要进行“汇总”了：
下面的函数就可以利用基于adaboosttrainDS()中的弱分类器对数据进行分类了。

1
2
3
4
5
6
7
8
9
10
11
12
def adaclassify(dattoclass,classifierarr):
    datamatrix=mat(dattoclass)
    m=shape(datamatrix)[0]
    aggclassest=mat(zeros((m,1)))
    for i in range(len(classifierarr)):
        classest=stumpclassify(datamatrix,
                               classifierarr[i]['dim'],
                               classifierarr[i]['thresh'],
                               classifierarr[i]['ineq'])
        aggclassest+=classifierarr[i]['alpha']*classest
        print(aggclassest)
    return sign(aggclassest)

文件载入与自检特征：

1
2
3
4
5
6
7
8
9
10
11
12
def loadDataSet(fileName):
    numFeat = len(open(fileName).readline().split('\t'))
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = []
        curLine = line.strip().split('\t')
        for i in range(numFeat - 1):
            lineArr.append(float(curLine[i]))
        dataMat.append(lineArr)
        labelMat.append(float(curLine[-1]))
    return dataMat, labelMat

其他分类度量指标
之前的分类器我们基本都是基于错误率来衡量成功程度的。
错误率也就是分类错误的占总测试样例中的比例。错误率越低，我们的分类器越成功。
实际上，这样的度量遮盖了样例如何被分错的事实。
接下来，我们使用一个名叫混淆矩阵的工具来更好的理解分类中的错误。
下面这个图是关于在房子周围可能发现动物类型的预测。

很显然，一个完美的分类器应当是使得这个矩阵的非对角元素全为0。
接下来，考虑一个二分类的混淆矩阵：

通过这个矩阵，我们可以定义一些概念：
将一个正例判为正例，即会产生一个真正例，也称真阳。
将一个反例正确地判定为一个反例，则认为产生了一个真反例，也称真阴。
在分类中，某个类别的重要性高于其他类别的时候，就可以定义出多个比错误率更优秀的
的新指标。
第一个指标称为正确率，表示真阳占所有预测为正例的比例。
第二个指标称为召回率，表示真阳站所有真实结果为正例的比例。
同时想要达到高正确率和高召回率是困难的。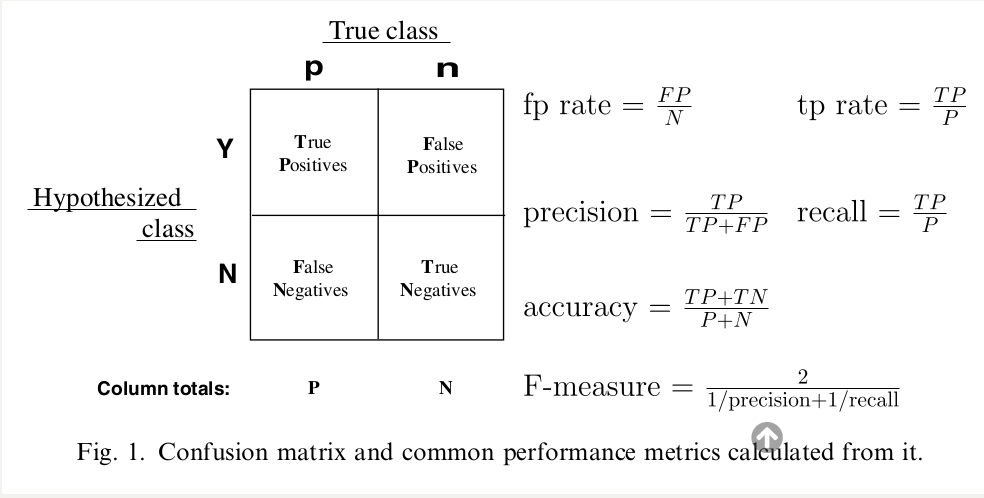

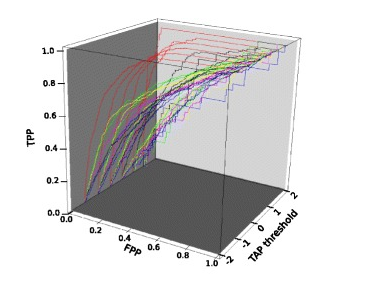
另一个用于度量分类中非均衡性的工具是ROC曲线，ROC代表接收者操作特征，
ROC曲线是根据一系列不同的二分类方式，以真阳率为纵坐标，假阳率为横坐标绘制的。
一般的评价方法是将我们的结果分为两类，然后进行评估，ROC曲线的评价方式与一般的
最大的区别在于可以根据实际情况，我们可以把实验成果划分为多个有序的分类序列，再
进行分析。
通过ROC曲线图像，我们可以比较不同分类器的优劣，将不同算法得到的曲线绘制到同一个坐标
系当中，很清楚就能判断出孰优孰劣，越是靠近左上角部分的曲线那么肯定更优秀咯。
同样，这个曲线是根据阈值变化来绘制曲线的，因此我们同时可以根据不同的阈值来使用表现最
好的分类器，将他们组合起来可能会得到更好的结果。
我们可以根据曲线下面积(AUC)来比较不同的ROC曲线，一个完美的分类器AUC值为1，而随机猜测
的则为0.5，似乎符合我们对概率的一般印象。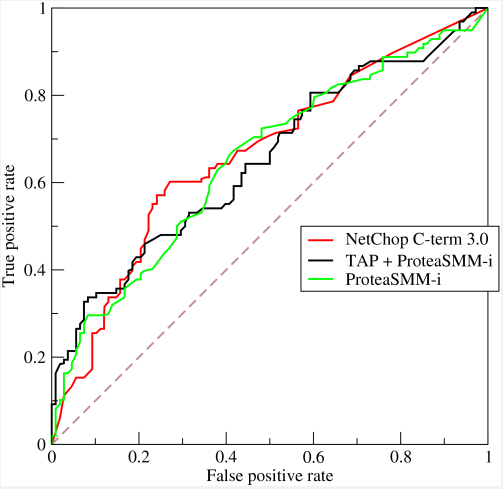

上图显示了蛋白质水解的酶体消化模式的提取，上图中有四个重要的点：
(0.0,1.0):超级完美的分类器。
(1.0,0.0):成功避开了所有的正确答案的分类器。。自不必多言了。。
(1.0,1.0):分类器预测所有样本都为正样本。
(0.0,0.0):分类器预测所有样本都为负样本。
还有一条虚线，就是随机猜测咯，大概有一半猜对，一半猜错。
其实相较混淆矩阵，我们对ROC可以有一种感受，就是其实相当于将离散的布尔值连续化了，
就像平时我们做出决断并不是之后好坏一样，可能在不同决策水平上，会得到不大一样的结果，
这种结果会依赖于决策水平。
那么如何绘制一条ROC曲线呢。
最简单直白的思路，取点描线。
因此必须知道每个样本被判断为阳性或者阴性的可信赖程度。
分类器有一个重要的功能就是概率输出，也就是描述一个样本有多大的概率属于正样本，
有多大的概率属于负样本，例如朴素贝叶斯告诉了我们一个可能性，Logistic回归给出一个
数值输入到Sigmoid()函数当中，SVM中也会计算出一个这样的值输入到sign()函数当中。
这些值就可以用于衡量这个分类器的得出的结果值不值得信赖。
为了创建ROC曲线，我们会先做一个排序，从排名最低的样例开始，排名更低的判定为反例，
排名更高的被判定为正例。然后将这个最低的移到次低的样例中去，如果属于正例，修改
真阳率，输入反例，对假阴率进行修改。
其实相当于我们设计了一个cursor，从排名最低的开始，在cursor指在某个被排列项的时候，
都将其作为一个阈值，然后比它排名高的自然可看作正样本，反之。
下面举了这样一个例子，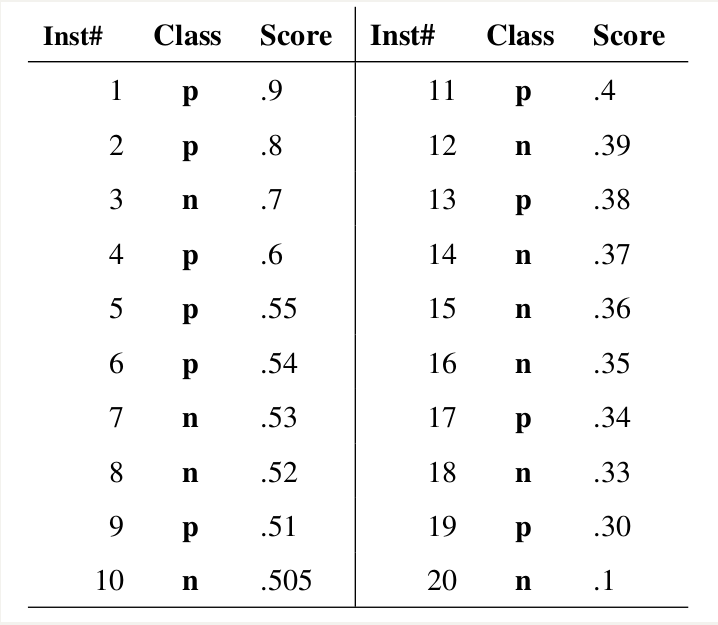

其中class为p即为正样本，为n即为负样本，score是每个测试样本属于正样本的概率，也就是
我们相信其为正样本的可信赖度。
那么以第5个样本为例，其概率为0.55，那么很显然如果我们将其作为阈值，那么样例1，2，3，
4都可以看作正样本，其他的都是负样本，cursor到达一个样例的时候，都会得到一组FPR和
TPR，那么上面这个例子就可以得到20组值对。
绘制到图上：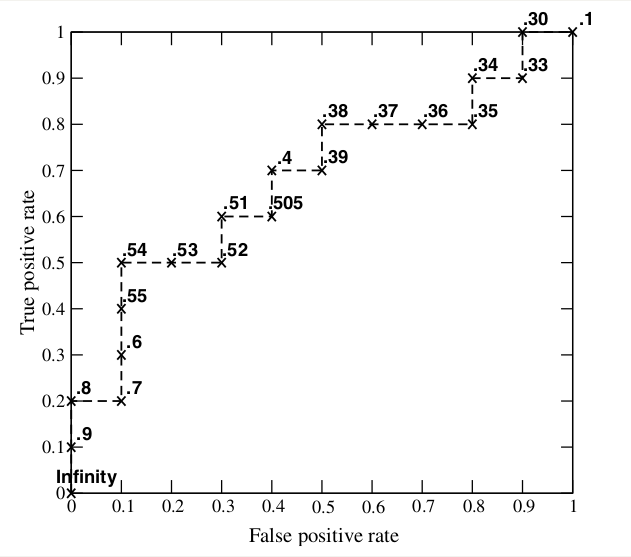

接下来，我们将绘制ROC曲线和计算AUC的代码加入：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def plotROC(predstrengths,classlabels):
    import matplotlib.pyplot as plt
    cur={1.0,1.0}
    ySum=0.0
    numPosClas=sum(array(classlabels)==1.0)
    yStep=1/float(numPosClas)
    xStep=1/float(len(classlabels)-numPosClas)
    sortedIndicies=predstrengths.argsort()
    fig=plt.figure()
    fig.clf()
    ax=plt.subplot(111)
    for index in sortedIndicies.tolist()[0]:
        if classlabels[index]==1.0:
            delX=0;delY=yStep
        else:
            delX=xStep;delY=0
            ySum+=cur[1]
        ax.plot([cur[0], cur[0] - delX], [cur[1], cur[1] - delY], c='b')
        cur = (cur[0] - delX, cur[1] - delY)
    ax.plot([0, 1], [0, 1], 'b--')
    plt.xlabel('False Positive Rate');
    plt.ylabel('True positive Rate')
    plt.title('ROC curve for AdaBoost Horse colic Detection System')
    ax.axis([0, 1, 0, 1])
    plt.show()
    print("the Area Under the Curve is:", ySum * xStep)

基于代价函数的分类器决策控制
我们上面介绍了通过调节分类器的阈值来处理非均匀代价问题的方法，
除此之外，我们还有一些其他的方法，其中的一种被称作代价敏感学习。
有如下两个代价矩阵：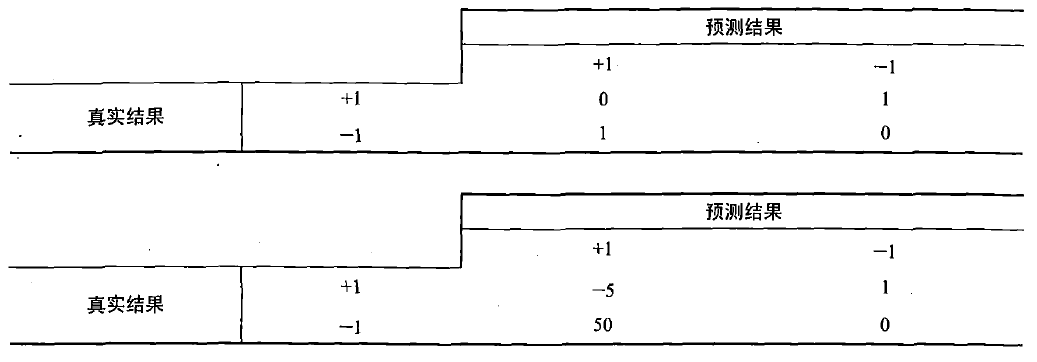

第一张表是目前为止分类器的代价矩阵，那么总代价可以计算：

1
TP*0+FN*1+FP*1+TN*0

同理第二张表可以计算：

1
TP*(-5)+FN*1+FP*50+TN*0

采用第二张表，分类错误的代价也是不同的。那么在我们构建分类器的时候，如果知道这些代价值，
就可以选择代价最小的分类器了。
在分类算法中，有很多方法可以引入代价信息。
在adaboost中，可以依据代价函数对权重向量D进行调整。
在朴素bayes中，可以选择具有最小期望代价而不是最大概率的类别作为结果。
在SVM中，可以在代价函数中对不同类别选择不同的参数C。
这些做法会给予较小的类更大的权重，即在训练中，小类只允许有更少的错误。

处理非均匀问题的数据抽样
另一种对非均匀问题调节分类器的方法，就是从输入原料着手，对训练数据进行改造加工。
可以通过两种方式实现：
过抽样：复制样例。
欠抽样：删除样例。
我们在分类过程中会有一些罕见的样例需要识别，
而这些比较特殊的罕见的样例反而会裹挟着更重要的东西，因此我们需要保留更多的信息。
那么我们对罕见样例进行过抽样处理，对那些相反的采取欠抽样。
这其中也存在缺点，我们需要了解哪些是可以剔除的，因为在某些剔除样例中也可能携带了
剩余样例中不包含的有价值信息。
我们可以采取一种方法，就是选择那些离决策边界较远的进行剔除。
例如在信用卡欺诈案例当中，可能有50例属于欺诈交易(正例，罕见样例)，
有5000例属于正常交易(反例)，如过为了达到平衡对反例进行欠抽样，那么就要删掉4950例，
而这些被删掉的样例中可能含有很多有价值信息。那么为了避免这种极端的产生，我们最好还是
反例欠抽样和正例过抽样混合的方法更好。
对正例进行过抽样，我们可以复制已有样例，也可以加入已有样例的相似样例，一种方式是加入
已有数据点的插值点，但是这可能会导致过拟合的问题。
感谢博主孔明的文章：http://alexkong.net/2013/06/introduction-to-auc-and-roc/

赏

谢谢你请我吃糖果

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

很惭愧<br><br>只做了一点微小的工作<br>谢谢大家