<学习笔记> 堆排序

2017-10-04

堆可以分为最大堆最小堆，是一棵完全二叉树。我们如果想要对一个序列进行非递减的排序，需要使用的是最大堆的结构。
堆排序可以分为两个步骤：
1.根据初始输入数据，形成初始堆；
2.通过一系列的元素交换和重新调整进行排序；
我们要进行堆排序，首先就要建立的我们的工具，最大堆。建堆的核心在于对它的调整，使我们的二叉树满足每个子节点的值都不大于其父节点的值。
调堆的过程要从最后一个非叶子节点开始。
假定有序列1 7 6 4 3 5 2 9 8；
那么我么要经历以下变换：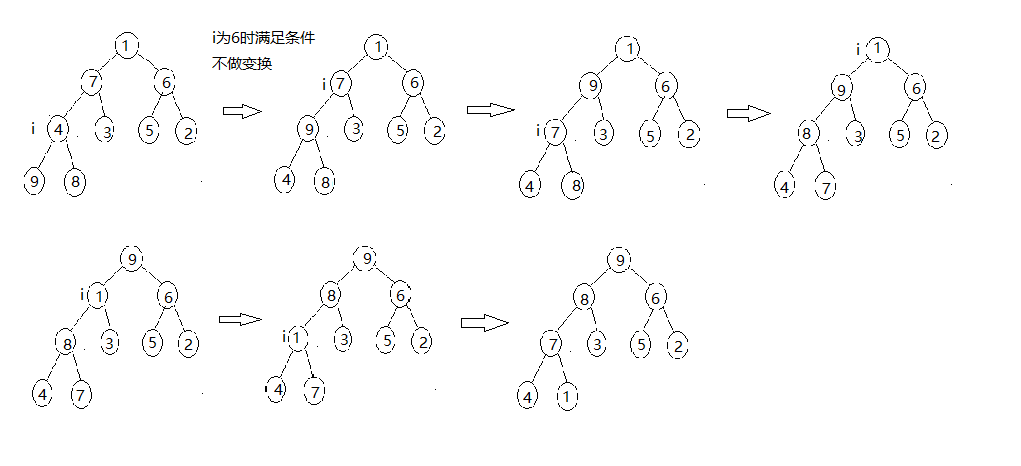

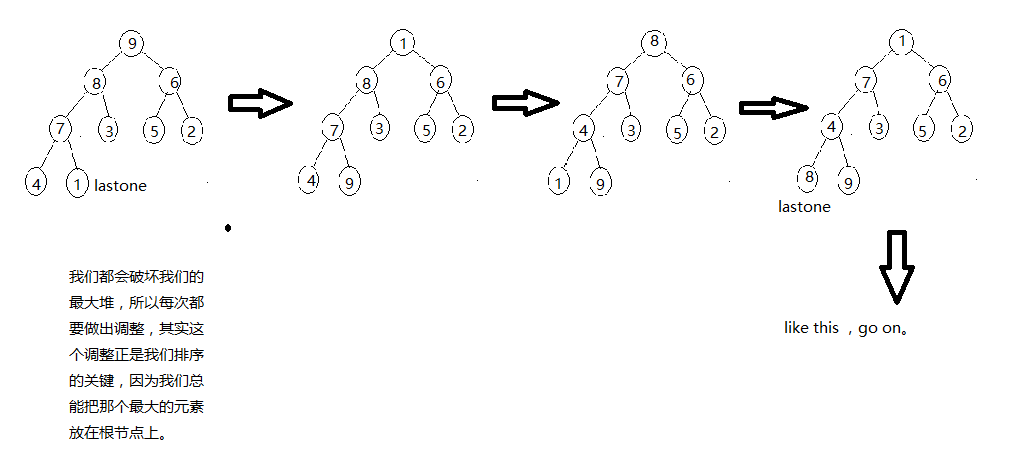
那么我们可以用以下代码进行调堆：

void swap(int &a,int &b){     //元素交换；
  int temp;
  temp=a;
  a=b;
  b=temp;
}
void adjheap(int list[],int heaplen){
  for(int i=heaplen/2;i>=0;i--){
    getmaxheap(list,heaplen,i);     //建堆入口；从第一个非叶子节点开始；
  }
}
void getmaxheap(int list[],int heaplen,int i){
  int left=2*i;
  int right=2*i+1;   //获取左子节点和右子节点的索引；
  int max=i;         //假设现在最大的节点是此时的父节点；
  if(i<=heaplen/2){       //i的边界，也就是第一个非叶子节点；
    if(left<=heaplen&&list[left]>list[max]){
      max=left;           //左子节点比此时假设的大；
    }
    if(right<=heaplen&&list[right]>list[max]){
      max=right;          //右子节点比此时假设的大；
    }
    if(max!=i){           //如果此时最大的不是最初假设的父节点；
      swap(list[max],list[i]);    //交换子节点和父节点的位置；
      getmaxheap(list,heaplen,max);   //向下递归，将目前的子节点当作父节点来进行相同的比较，直到到达i的边界；
    }
  }
}
void heapsort(int list[],int heaplen){
  adjheap(list,heaplen);     //在排序前进行堆的建立；
  for(int i=heaplen-1;i>=0;i--){
    swap(list[0],list[i]);   //将最后一个元素与第一个交换；
    getmaxheap(list,i-1,0);  //再进行堆的调整，变为我们所要的最大堆；
    //很明显，堆排序的过程就是最大堆的不断重建和根元素和当前最后一个元素交换的过程；
  }
}