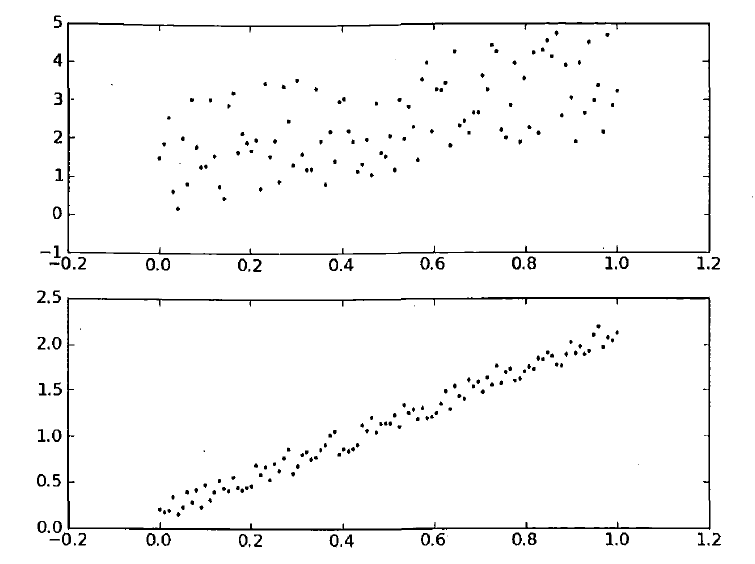
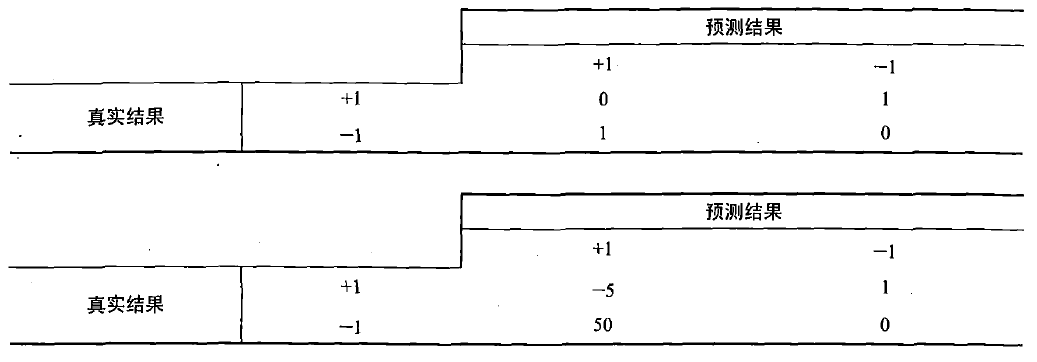
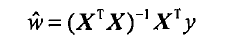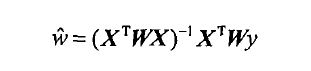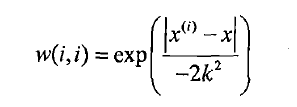背包问题描述:
有n个物品,每个物品有2个属性:重量w和价值v。指定一个背包,该背包能承受的最大重量为W,
对每个物品来说,只有放入背包和不放入背包2种选择。
求解:如何在不超过该背包最大承重W的前提下,使得放入物品的总价值V最大?
曾经用动态规划和分支限界搞定过,换个方法玩一下。
达尔文说过:能够生存下来的往往不是最强大的物种,也不是最聪明的物种,而是最能适应环境的物种。
这个算法就是这么来的,物竞天择,适者生存。
那么这个算法就有四个基本的要点:
种群:由个体组成,每个个体携带有染色体和基因。
选择:优胜劣汰。
交叉:通过交叉来进行基因的重组。
变异:基因概率突变。
1.初始化:
那么背包问题如何与生物这个遗传进化的过程相联系呢。
我们将染色体用二进制,那么0表示物品不装入背包,1表示物品装入背包。
在进化过程当中,0即为基因丢失,1即为基因保留。
个体的适应性用适应度衡量,背包问题中也就是我们背包中的价值总和越高越好,但是这里的总重量
不可以超过背包的预设重量,进化不可逆自然规律而行。
2.选择:
从总体中选择合适的个体,让其进行交配。
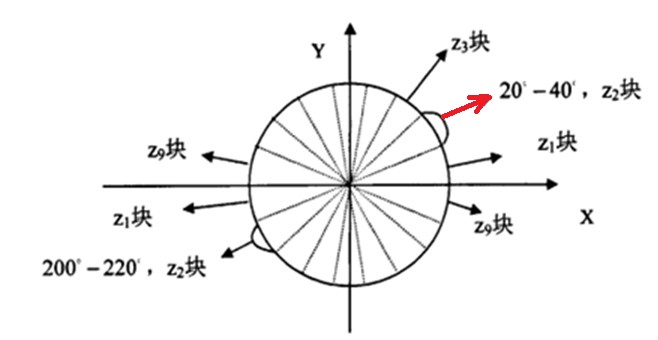
这里为了保证生物的多样性,不至于在几代之后差异过小,那么选用轮赌法。
也就是相当于将一个圆分为总体中染色体数量的n个部分,每条染色体所占圆的面积由其适应度按比例来
界定。
那么为这个圆设置一个指针,轮盘旋转,当轮盘停下的时候指针所指即为所选择个体,
那么重复这个过程两次,即可选中两个亲本。
3.交叉:
交叉分为很多中,单点交叉,多点交叉,均匀交叉,这里选择单点交叉。
随机在染色体上选择一个交叉点,然后交换交叉点前后的部分,形成两个新的个体。
表现在这里,就是我们的二进制序列上选择一个分界点,亲本的前半部分和后半部分分别重新组合即可。
4.变异:
生物在进化过程当中,不仅有遗传,还有变异。
体现在我们这里就是二进制序列上的某一位概率的发生改变。
这个过程进行完,那么就基本完成了一个进化的过程,也就是一轮繁殖。
那么我们什么时候找到最好的那一代呢,也就是进化最完全的那一代呢。
也就是如何找到最佳的适应水平。
一般有如下几种适应条件:
1.再进行繁殖不会发生太大的改变,趋于稳定。
2.事先规定迭代次数。
3.事先预定最佳的适应度。
以下即为模拟过程代码: